Attention Is All You Need
-
Attention Is All You Need
-
torch.nn.Transformer
-
torch.nn.MultiheadAttention
keywords to search:
RNN,
LSTM,
Gated RNN
-
Introduction
-
Recurrent models typically factor computation along the symbol positions of the input and output sequences.
Inherently seqquential nature of Recurrent model precludes parallelization within training examples,
which becomes critical at longer sequence lengths, as memory constraints limit batching across examples.
-
Attention mechanisms have become an integral part of sequence modeling and transduction models in various tasks,
allowing modeling of dependencies without regard to their distance in the input or output sequences.
-
In this work we propose the Transformer, a model architecture eschewing recurrence and instead relying entirely on an attention mechanism to draw global dependencies between input and output.
-
Model Architecture
-
Most competitive neural sequence transduction models have an encoder-decoder structure.
The encoder maps an input sequence of symbol representations \((x_1, \, ..., \, x_n) \) to a sequence of continuous representations \(z = (z_1, \, ..., \, z_n) \).
Given \(z\), the decoder then generates an output sequence \((y_1, \, ..., \, y_m ) \).
-
At each step the model is auto-regressive, consuming the previously generated symbols as additional input when generating the next.
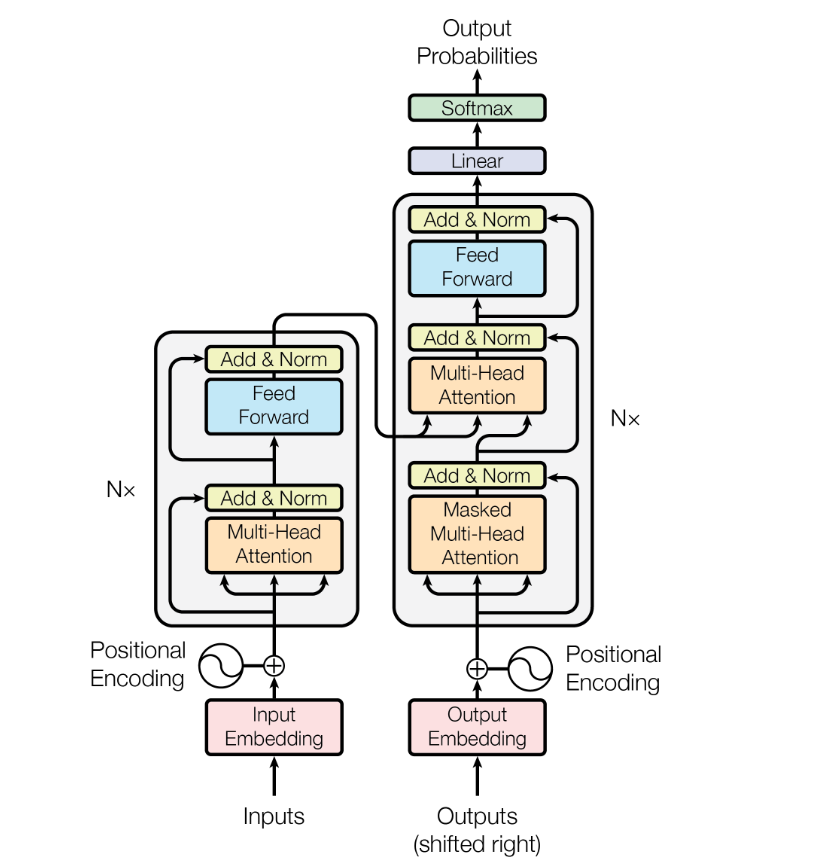 Transformer model architecture
Transformer model architecture
-
The Transformer follows this overall architecture using stacked self-attention and point-wise (position-wise),
fully connected layers for both the encoder and decoder, shown in the left and right halves of Figure 1, respectively.
-
Encoder and Decoder stacks
-
Encoder: Each layer has two sub-layers.
The first is a multi-head self-attention mechanism, and the second is a simple, position-wise fully connected feed-forward network.
We employ a residual connection around each of the two sub-layers, followed by layer normalization.
The output of each sub-layer is as:
\[
\,\\
\text{LayerNorm}(x + \text{Sublayer}(x))
\,\\
\]
-
Decoder: The decoder inserts a third sub-layer, which performs multi-head
attention over the output of the encoder stack.
Similar to the encoder, we employ residual connections around each of the sub-layers, followed by layer normalization.
The masking, combined with fact that the output embeddings are offset by one position, ensures that the
predictions for position \(i\) can depend only on the known outputs at positions less than \(i\).
-
Attention
-
An attention function can be described as mapping a query and a set of key-value pairs to an output,
where the query, keys, values, and output are all vectors.
The output is computed as a weighted sum of the values.
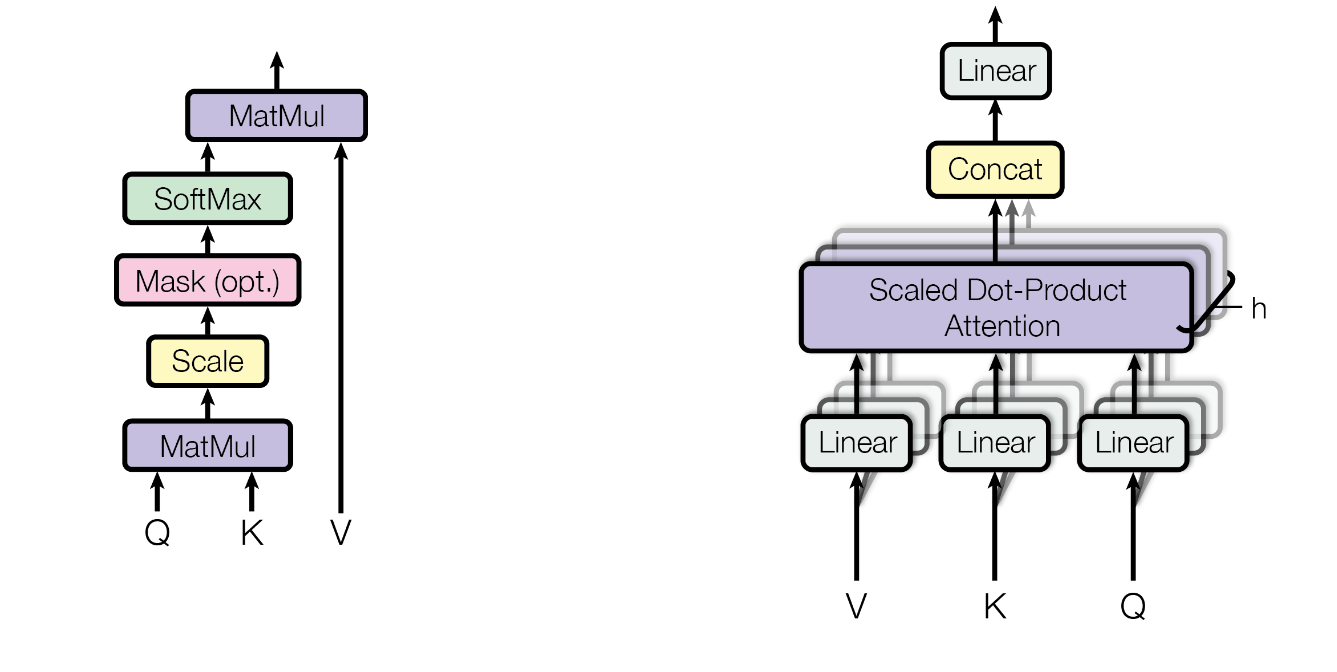 From the left, Scaled Dot-Product Attention · Multi-Head Attention
From the left, Scaled Dot-Product Attention · Multi-Head Attention
-
Scaled Dot-Product Attention
-
The input consists of queries and keys of dimension \(d_k\), and values of dimension \(d_v\).
We compute the dot products of the query with all keys, divide each by
\(\sqrt{d_k} \), and apply a softmax function to obtain the weights on the values.
\[
\,\\
\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V
\,\\
\]
-
Dot-product attention is identical to our algorithm, except for the scaling factor of \(\frac{1}{\sqrt{d_k}} \).
class ScaledDotProductAttention(nn.Module):
def __init__(self):
super().__init__()
self.softmax = nn.Softmax(dim=-1)
def forward(self, q, k, v):
attention = self.softmax(
torch.matmul(q, k.transpose(-1, -2)) # \(QK^{T}\)
/ torch.sqrt(torch.tensor(k.size(-1))) # \(\sqrt(d_{k})\)
)
return torch.matmul(attention, v)
Multi-Head Attention
-
Instead of performing a single attention function with dmodel-dimensional keys, values and queries,
we found it beneficial to linearly project the queries, keys and values \(h\) times with different,
learned linear projections to \(d_{k}\), \(d_{k}\) and \(d_{v}\) dimensions, respectively.
-
Multi-head attention allows the model to jointly attend to information from different representation
subspaces at different positions. With a single attention head, averaging inhibits this.
\[
\,\\
\text{MultiHead}(Q, K, V) = \text{Concat(head_1, ..., head_h)}W^O
\,\\
\]
where \(head_i = \text{Attention}(QW^Q_i, \, KW^K_i, \, VW^V_i) \).
-
In this work we employ \(h = 8\) parallel attention layers, or heads.
For each of these we use \(d_k = d_v = d_{model}/h = 64 \).
class MultiHeadAttention(nn.Module):
def __init__(self, h=8, d_model=512):
super().__init__()
self.h = h
self.d_model = d_model
self.d_k = d_model // h
self.linear_q = nn.Linear(d_model, d_model)
self.linear_k = nn.Linear(d_model, d_model)
self.linear_v = nn.Linear(d_model, d_model)
self.linear_o = nn.Linear(d_model, d_model)
self.scaled_dot_product_attention = ScaledDotProductAttention()
def forward(self, q, k, v):
qw = self.linear_q(q).reshape(q.shape[0], -1, self.h, self.d_k).transpose(1, 2)
kw = self.linear_k(k).reshape(q.shape[0], -1, self.h, self.d_k).transpose(1, 2)
vw = self.linear_v(v).reshape(q.shape[0], -1, self.h, self.d_k).transpose(1, 2)
attention_scores = self.scaled_dot_product_attention(qw, kw, vw).transpose(1, 2)
attention_output = self.linear_o(attention_scores.reshape(q.shape[0], -1, self.d_model))
return attention_output
Position-wise Feed-Forawrd Networks
-
In addition to attention sub-layers, each of the layers in our encoder and decoder contains a fully connected feed-forward network,
which is applied to each position separately and identically.
This consists of two linear transformations with a \(\text{ReLU}\) activation in between.
\[
\,\\
\text{FFN}(x) = \text{max}(0, xW_1 + b_1)W_2 + b_2
\,\\
\]
class FeedForward(nn.Module):
def __init__(self, d_model, d_hidden):
super().__init__()
self.d_model = d_model
self.d_hidden = d_hidden
self.ff = nn.Sequential(
nn.Linear(self.d_model, self.d_hidden),
nn.ReLU(),
nn.Linear(self.d_hidden, self.d_model)
)
def forward(self, x):
return self.ff(x)
Positional Encoding
-
Since our model contains no recurrence and no convolution, in order for the model to make use of the
order of the sequence, we must inject some information about the relative or absolute position of the
tokens in the sequence.
-
The positional encodings have the same dimension \(d_{model}\) as the embeddings, so that the two can be summed.
\[
\,\\
\begin{aligned}
PE_{(pos, 2i)} &= sin(pos / 10000^{2i/d_{model}}) \\
PE_{(pos, 2i + 1)} &= cos(pos / 10000^{2i/d_{model}})
\end{aligned}
\,\\
\]
where \(pos\) is the position and \(i\) is the dimension.
(
\(pos = 0\)인 경우 첫 번째 단어, \(pos = 1\)인 경우 두 번째 단어.
\(d_{model} = 512\)인 경우 \(i\) 는 0 ~ 511.
\(pos\)를 큰 수로 나누어 노말라이즈?
임베딩 된 단어 벡터들이 서로 가까운 위치에 있으면 비슷한 주기의 포지셔널 인코딩 값을 가지므로,
단어벡터와 포지셔널 인코딩 값이 더해졌을 때 유사한 값이 됨
)
class PositionalEncoding(nn.Module):
def __init__(self, d_model, max_sequence_len=1000):
super().__init__()
self.d_model = d_model
self.max_sequence_len = max_sequence_len
self.positional_encoding_table = torch.zeros(self.max_sequence_len, self.d_model)
pos = torch.arange(0, self.max_sequence_len).unsqueeze(1)
_2i = torch.arange(0, self.d_model)[0::2]
self.positional_encoding_table[:, 0::2] = torch.sin(pos / 10000 ** (_2i / self.d_model))
self.positional_encoding_table[:, 1::2] = torch.cos(pos / 10000 ** (_2i / self.d_model))
def forward(self, x):
return x + self.positional_encoding_table[:x.size(1), :]
Encoder and Decoder Layers
class EncoderLayer(nn.Module):
def __init__(self, h=8, d_model=512, d_hidden=2048):
super().__init__()
self.h= h
self.d_model= d_model
self.d_hidden= d_hidden
self.self_attention = MultiHeadAttention(h=h, d_model=d_model)
self.layer_norm_1 = nn.LayerNorm(d_model)
self.feed_forward = FeedForward(d_model=d_model, d_hidden=d_hidden)
self.layer_norm_2 = nn.LayerNorm(d_model)
def forward(self, x):
attention_output = self.self_attention(x, x, x)
x = self.layer_norm_1(x + attention_output)
ff_output = self.feed_forward(x)
x = self.layer_norm_2(x + ff_output)
return x
class DecoderLayer(nn.Module):
def __init__(self, h=8, d_model=512, d_hidden=2048):
super().__init__()
self.h= h
self.d_model= d_model
self.d_hidden= d_hidden
self.self_attention = MultiHeadAttention(h=h, d_model=d_model)
self.layer_norm_1 = nn.LayerNorm(d_model)
self.cross_attention = MultiHeadAttention(h=h, d_model=d_model)
self.layer_norm_2 = nn.LayerNorm(d_model)
self.feed_forward = FeedForward(d_model=d_model, d_hidden=d_hidden)
self.layer_norm_3 = nn.LayerNorm(d_model)
def forward(self, x, encoded_x):
attention_output = self.self_attention(x, x, x)
x = self.layer_norm_1(x + attention_output)
cross_attention_output = self.cross_attention(x, encoded_x, encoded_x)
x = self.layer_norm_2(x + cross_attention_output)
ff_output = self.feed_forward(x)
x = self.layer_norm_3(x + ff_output)
return x
Why Self-Attention
-
Parallelization: Self-attention can connect all positions with a constant number of sequential steps, while recurrent layers require sequential operations across the entire sequence.
-
Interpretability: Self-attention also enhances model interpretability by allowing us to observe how information is distributed across positions.
( ... )